Free math answers are available on all types of math questions such as basic math, numbers, algebra, logarithm, trigonometry, and pre-calculus homework questions with step-by-step.
In free math answers, these are the questions asked by the students to show it in step-by-step solution.
1. In a group of cows and chickens, the number of legs was 14 more than twice the number of heads. The number of cows was:
(a) 5, (b) 7, (c) 10, (d) 12, (e) 14
Solution:
Let the number of cows be x and their legs be 4x.
Let the number of chicken be y and their legs be 2x.
Total number of legs = 4x + 2y.
Total number of heads = x + y.
The number of legs was 14 more than twice the number of heads.
Therefore, 2 × (x + y) + 14 = 4x + 2y.
or, 2x + 2y + 14 = 4x + 2y.
or, 2x + 14 = 4x [subtracting 2y from both sides].
or, 14 = 4x – 2x [subtracting 2x from both sides].
or, 14 = 2x.
or, x = 7 [dividing by 2 on both sides].
Therefore, the number of cows = 7.
Answer: (b)
2. The roots of the equation ax2 + bx + c = 0 will be reciprocal if:
(a) a = b, (b) a = bc, (c) c = a, (d) c = b, (e) c = ab.
Solution:
Let k be one of the root of the given equation.
According to the problem,
1/k will be the other root of the given equation.
We know that, product of the roots of the equation = c/a.
Therefore, k × 1/k = c/a.
or, 1 = c/a.
or, a = c [multiplying a on both sides].
The roots of the equation ax2 + bx + c = 0 will be reciprocal if a = c.
Therefore, a = c or c = a.
Answer: (c)
3. If 8 ∙ 2x = 5(y+8), then when y = -8, x =
(a) -4, (b) -3, (c) 0, (d) 4, (e) 8
Solution:
8 ∙ 2x = 5(y+8).
or, 8 ∙ 2x = 5(-8+8).
or, 2x = 50.
or, 2x = 1 [anything to the power 0 is 1 then, 50 = 1].
Taking log on both sides,
log 2x = log 1.
or, x log 2 = 0 [since log 1 = 0].
or, x = 0/log 2 [dividing log 2 on both sides].
Therefore, x = 0.
Answer: (c)
4. A circle of radius 10 inches has its center at the vertex C of an equilateral triangle ABC and passes through the other two vertices. The side AC extended through C intersects the circle at D. The number of degrees of angle ADB is:
(a) 15, (b) 30, (c) 60, (d) 90, (e) 120
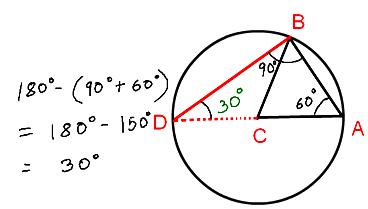
Answer: (b)5. The expression 1 – 1/(1 + √3) + 1/(1 – √3) equals:(a) 1 – √3, (b) 1, (c) – √3, (d) √3, (e) 1 + √3.Solution:
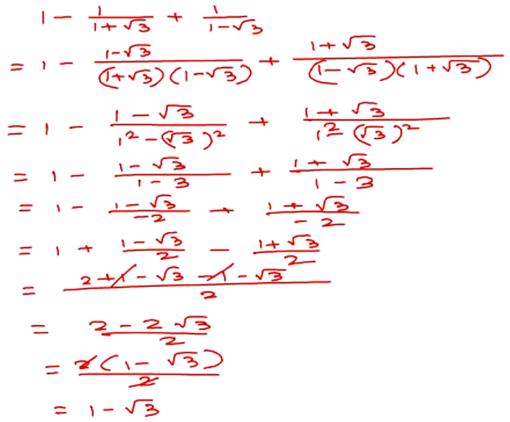
6. If x-1 – 1 is divided by x – 1 the quotient is:
(a) 1, (b) 1/(x-1), (c) – 1/(x-1), (d) 1/x, (e) – 1/x
Solution:
x-1 – 1 is divided by (x – 1)
= x-1 – 1 × 1/(x-1)
= 1/x – 1 × 1/(x-1)
= (1 – x/x) × 1/(x-1)
= – (1 – x)/x × 1/(x-1)
= – 1/x [cancel x – 1 from the numerator and denominator].
Answer: (e)
7. The root(s) of 15/(x2 – 4) – 2/(x – 2) = 1 is (are):
(a) -5 and 3, (b) ± 2, (c) 2 only, (d) -3 and 5, (e) 3 only.
Solution:
15/(x2 – 4) – 2/(x – 2) = 1.
15/(x2 – 22) – 2/(x – 2) = 1.
15/(x + 2)(x – 2) – 2/(x – 2) = 1.
[15 – 2(x + 2)]/[(x + 2)(x – 2)] = 1.
[15 – 2x – 4] /[(x + 2)(x – 2)] = 1.
[11 – 2x]/[(x + 2)(x – 2)] = 1.
11 – 2x = (x + 2)(x – 2).
11 – 2x = x2 – 4.
x2 – 4 = 11 – 2x.
x2 + 2x – 4 – 11 = 0.
x2 + 2x – 15 = 0.
x + 5) (x – 3) = 0.
x + 5 = 0 or, x – 3 = 0
x = -5 or, x = 3.
Therefore, x = -5 and 3.
Answer: (a)
8. A 7-in. pizza costs $8 and a 14-in. pizza costs $20. Tommy says the smaller pizza is a better buy because the larger pizza is twice as big and more than twice as expensive. Do you agree with his reasoning? If not, explain why not.
Solution:
No, a pizza looks like a circle.
And we know that area of a circle depends on the radius.
Area of a circle = πr2, here pi (π) is constant.
So, we can clearly say that area of a circle is proportional to the square of the diameter.
Similarly, the cost a pizza depends on its area not its diameter.
9. Suppose that Jody drove 80 miles in 2 hours. Dividing 80 by 2 tells us how many miles Jody drove in each hour. The units for this rate are miles per hour (mi/hr). If we divide 2 by 80 what information would this give us? Give an interpretation of the rate. What units would be used for this rate?
Solution:
We know that, speed = distance/time.
When total distance is divided by total time we get the speed.
Here, speed = distance covered in 1 hour.
According to the question,
Total distance 80 miles divided by total time 2 hours = 80/2.
miles/hour = 40 mile/hour.
Therefore, Jody drove 40 miles in 1 hour.
But if we divide total time by total distance then, we get time taken to cover 1 mile.
Similarly, if we divide 2 by 80 then, we get time taken to cover 1 mile.
Therefore, unit used for this case = hours/mile.
10. 19/6 = 4/27. Which method did you use to determine whether this proportion is true or false?
Solution:
19/6 = 4/27.
Cross multiplication:
19 × 27 = 513.
6 × 4 = 24.
We see that 513 are not equal to 24.
Therefore, we determine 19/6 = 4/27 is not proportion so, the answer is false.
11. On Thursday Mabel handled 90 transactions. Anthony handled 10% more transactions than Mabel, Cal handled 2/3rds of the transactions that Anthony handled, and Jade handled 16 more transactions than Cal. How much transactions did Jade handled?
Solution:
Mabel handled 90 transactions
Anthony handled 10% more transactions than Mabel
Anthony = 90 + 90 × 10%
= 90 + 90 × 0.10
= 90 + 9
= 99
Cal handled 2/3rds of the transactions than Anthony handled
Cal = 2/3 × 99
= 66
Jade handled 16 more transactions than Cal.
Jade = 66 + 16
= 82
Jade handled = 82 transactions.
Answer: 82
12. If a man buys 20 lollipops for $90 and sold them for $2 dollars determine his loss.
Solution:
Cost of 20 lollipops = $90
Sold each lollipop for $2
So he sold 20 lollipops for $(20 × 2) = $40
Loss = $(90 – 40) = $50
Therefore, loss = $ 50.
13 . If C is a whole number, C+1 is a whole number after that. If A is a whole number, what is a whole number before that?
Solution:
We know that the number ‘0’ together with the natural numbers gives us the numbers 0, 1, 2, 3, 4, 5, …………… which are called whole numbers.
If A is a whole number and it is greater than 0 then the whole number before that is A – 1, which will always be a whole number.
Again, when A is a whole number and it is equal to 0 then the whole number before that is A – 1 which means 0 – 1 = -1, which is not a whole number.
Therefore, if A is a whole number then the number before that will not always be a whole number.
14. Solve and leave answer in fraction
– (2-5/4)/9
Solution:
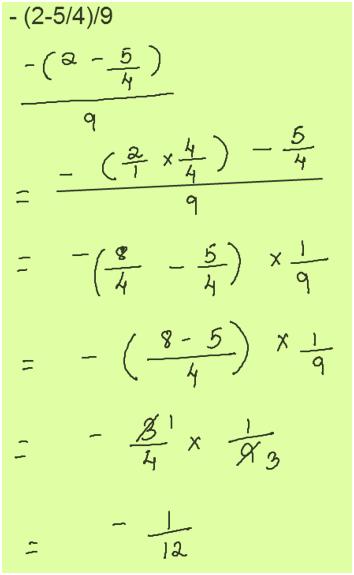
Answer: -1/12
15. Divide the cancelling out all common factors
Solution:
-((1-13/8)/10/24)
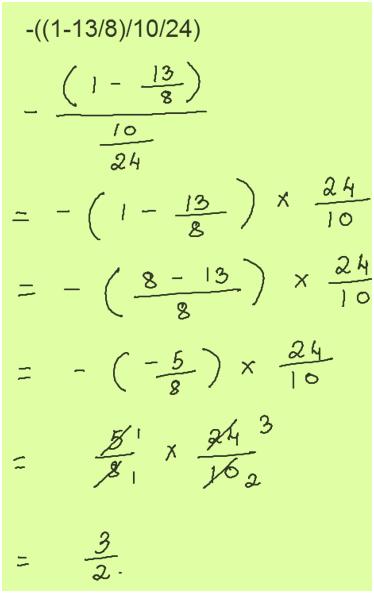
Answer: 3/2
16. The annual cost of owning and operating a car, C dollars, is a linear function of the distance, d kilometers, it is driven.
c = md + b
The cost is $4600 for 10 000 km and $9100 for 25 000 km.
(a) Determine the values of m and b.
(b) Write c as a function of d.
Solution:
(a)
c = md + b
The cost is $ 4600 for 10 000 km
4600 = m (10 000) + b
10 000 m + b = 4600
b = -10 000 m + 4600 ——- (i)
The cost is $ 9100 for 25 000 km
9100 = m (25 000) + b
9100 = 25 000 m + b
25 000 m + b = 9100
b = -25 000 m + 9100 ——— (ii)
From equation (i) and (ii) we get;
-10 000 m + 4600 = -25 000 m + 9100
-10 000 m + 25 000 m = 9100 – 4600
15 000 m = 4500
m = 4500/15 000
m = 3/10
m = 0.3
Now, put the value of m = 0.3 in equation (i) we get;
b = -10 000 (0.3) + 4600
b = -3000 + 4600
b = 1600
Answer: m = 0.3 and b = 1600
(b) c = md + b
m = 0.3
b = 1600
c = 0.3d + 1600
Answer: c = 0.3d + 1600
17. Solve using synthetic division or long division(x2 + 13x + 40) ÷ (x + 8)
Solution:
We solved the division in both the ways;
(x2 + 13x + 40) ÷ (x + 8) by using synthetic division
Quotient = x + 5
Remainder = 0
OR
(x2 + 13x + 40) ÷ (x + 8) by using long division
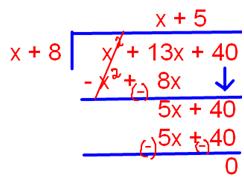
Quotient = x + 5
Remainder = 0
Answer: x + 5
18. Solve using on synthetic division or long division (2x2 – 23x + 63) ÷ (x – 7)
Solution:
We solved the division in both the ways;
(2x2 – 23x + 63) ÷ (x – 7) by using synthetic division,
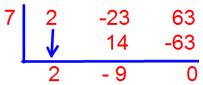
Quotient = 2x – 9
Remainder = 0
OR
(2x2 – 23x + 63) ÷ (x – 7) by using long division
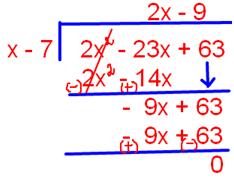
Quotient = 2x – 9
Remainder = 0
Answer: 2x – 9
19. Let f(x) = 4x3 + 7x2 – 13x – 3 and g(x) = x + 3. Find f(x)/g(x)
Solution:
f(x) = 4x3 + 7x2 – 13x – 3
g(x) = x + 3
f(x)/g(x) = (4x3 + 7x2 – 13x – 3)/(x + 3)
We solved the division in both the ways;
(4x3 + 7x2 – 13x – 3) ÷ (x + 3) by using synthetic division
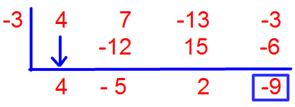
Answer:
Quotient = 4x2 – 5x + 2
Remainder = -9
OR
(4x3 + 7x2 – 13x – 3) ÷ (x + 3) by using long division

Answer:
Quotient = 4x2 – 5x + 2
Remainder = -9
20. Let f(x) = 3x3 – 4x – 1 and g(x) = x + 1. Find f(x)/g(x)
Solution:
f(x) = 3x3 – 4x – 1
g(x) = x + 1
f(x)/g(x) = (3x3 – 4x – 1)/(x + 1)
We first need to rearrange all the terms of the dividend according to descending powers of x. The dividend then becomes 3x3 – 4x – 1, with 3 understood as the coefficient of the first term. No x2 term is there in the polynomial, but we take a zero as a place holder in the x2 position, so the dividend is written as 3x3 + 0x2 – 4x – 1.
We solved the division in both the ways;
(3x3 + 0x2 – 4x – 1) ÷ (x + 1) by using synthetic division
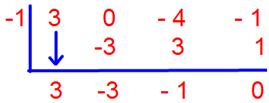
Quotient: 3x2 – 3x – 1
Remainder: 0
OR
No x2 term is there in the polynomial, but we take a zero as a placeholder in the x2 position, so the dividend is written as
3x3 + 0x2 – 4x – 1.
(3x3 + 0x2 – 4x – 1) ÷ (x + 1) by using long division

Quotient: 3x2 – 3x – 1
Remainder: 0
Answer: 3x2 – 3x – 1
21. Let f(x) = x4 – 8x3 + 16x2 – 19 and g(x) = x – 5. Find f(x)/g(x)
Solution:
f(x) = x4 – 8x3 + 16x2 – 19
g(x) = x – 5
f(x)/g(x) = (x4 – 8x3 + 16x2 – 19)/(x – 5)
We first need to rearrange all the terms of the dividend according to descending powers of x. The dividend then becomes x4 – 8x3 + 16x2 – 19, with 1 understood as the coefficient of the first term. No x term is there in the polynomial, but we take a zero as a place holder in the x position, so the dividend is written as x4 – 8x3 + 16x2 + 0x – 19.
We solved the division in both the ways;
(x4 – 8x3 + 16x2 + 0x – 19) ÷ (x – 5) by using synthetic division

Quotient = x3 – 3x2 + x + 5
Remainder = 6
OR
No x term is there in the polynomial, but we take a zero as a place holder in the x position, so the dividend is written as
x4 – 8x3 + 16x2 + 0x – 19.
(x4 – 8x3 + 16x2 + 0x – 19) ÷ (x – 5) by using long division

Quotient = x3 – 3x2 + x + 5
Remainder = 6
Answer:
Quotient = x3 – 3x2 + x + 5
Remainder = 6